Pišu: Dušan pavlović i Ivan Stanojević –
U ovom blogu odgovaramo na pitanje može li Demokratska stranka ponovo da se vrati na vrhunac na kome je bila 2008. godine. Odgovor obrazlažemo preko teoreme o srednjem glasaču (median voter theorem). Izlažemo najpre teoremu, a potom je primenjujemo na sadašnji stranački sistem u Srbiji.
Zamislite stranački sistem od samo dve stranke, 1 i 2. Teorema kaže da će tendencija stranaka biti da konvergiraju ka sredini političkog spektra. Bez ozbira na to da li su birači raspoređeni ravnomerno duž političkog spektra, ili ih ima najviše na sredini, za svaku stranku je uvek najbolje da se programski smesti negde u sredini političkog spektra.
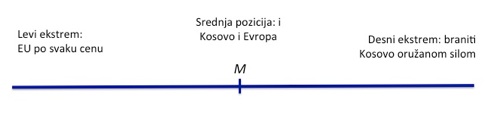
Pogledajmo prvi grafikon. Pretpostavite da politički kontinuum označava dve pozicije — Kosovo i EU. Na levom ekstremu su radikalni evropejci, na desnom radnikalni nacionalisti. Kako se krećete ka sredini spektra (tačka M), birači su sve umereniji i traže najbolje od oba sveta. Najviše glasova osvojiće stranka koja ubedi birače da će sprovesti politiku M.
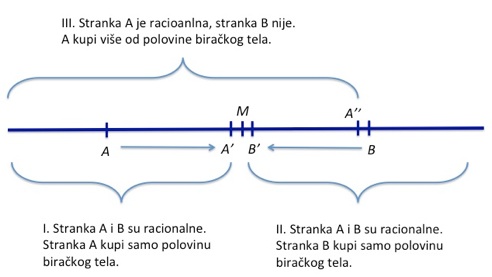
Pretpostavimo potom da stranka 1 započinje svoj politički život na poziciji A (vidi drugi grafikon ispod). Njoj je bolje da se pomeri ka poziciji A’, jer će tamo sigurno pokupiti sve birače od tačke A’ na levo, što čini otprilike polovinu biračkog tela (slučaj I, gde su obe stranke racionalne). Isto to važi i za stranku 2 koja započinje politički život na poziciji B (slučaj II). Ukoliko bi stranka 2 tvrdoglavo insistirala da ostane ne poziciji B (tj. da se ne pomeri ka B’), stranka 1 bi mogla da joj se približi još više, recimo u tačku A’’, i tako pokupi sve glasove od A’’ na levo, što čini više od polovine (slučaj III). Dakle, kada su racionalne, ni jedna stranka se neće udaljavati daleko od tačke M, jer tako rizikuje da izgubi glasove.
Postoji i drugi uslov pod kojim teorema funkcioniše: da bi stranke otprilike podjednako podelile biračko telo, moraju obe da budu otprilike podjednako uverljive da se zalažu za politiku sa pozicije M. Ako je stranka 1 ubedljivija od 2 da će sprovesti politiku M, onda nije važno da li se obe stranke nalaze blizu M. Stranka 1 će pokupiti više glasova.
Kako je DS postala najjača stranka 2008. godine? Tako što je ostala sama negde oko tačke M. Ona je najuverljivije zagovarala politiku “I Kosovo i Evropa” (drugo ime za politiku M). Jedno vreme se na tački M nalazila zajedno sa DSS-om (na izborima 2007. godine su imali približan broj glasova). A onda je DSS počeo naglo da se udaljava od tačke M, i počeo da se kreće ka tački B. Nakon toga DS je ostala sama na srednjoj poziciji i postala najjača stranka u Srbiji.
Može li DS povratiti popularnost iz 2008. godine? Smatramo da za sada ne može iz dva razloga. Prvo, sada DS na toj poziciji više nije sama — tu je SNS koji je učio iz odnosa DS i DSS-a, i 2008. godine počeo da radi isto što je 2004. godine počela da radi DS. Ali ne samo to — sada SNS deluje mnogo ubedljivije na toj poziciji od DS-a. Većini izgleda da će naprednjaci, pre nego demokrate, uvesti Srbiju u EU, rešiti pitanje Kosova i smanjiti korupciju. DS promenom lidera nije uspela da postane ubedljivija u tvrdnji da će sprovesti politiku M, a baš to je trebalo da bude smisao promene vođstva u stranci.
Ni to nije sve. DS se povremeno udaljava od sredine u pravcu oba ekstrema, kritikujući čas naprednjake zbog “popuštanja u kosovskoj politici”, čas zbog toga što “nisu dovoljno evropski orijentisani”. Svaki put kada tako nešto urade, DS ostavlja SNS samu u centru i time sebi zatvara vrata za povratak na pozicije iz 2008. godine.
DS-u, ali i drugim strankama koje pretenduju da izazovu SNS kao dominantnu stranku, potrebne su nove teme koje su važne za građane, kao i potencijalna rešenja koja bi bila bolja od onih koje nudi SNS. Na žalost pristalica DS i na sreću pristalica SNS, ni priče o povratku u devedesete, ni inicijativa za podizanje spomenika Zoranu Đinđiću nisu ta tema.